y=f(x) функциясы x нүктенің белгілі бір маңайында аңықталсын.
Аңықтама
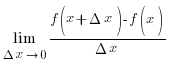 шегі бар болса онда бұл шек y=f(x) функциясының x нүктедегі туындысы деп аталады және
шегі бар болса онда бұл шек y=f(x) функциясының x нүктедегі туындысы деп аталады және 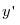 не
не 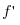 (x) деп белгіленеді.
(x) деп белгіленеді.
Яғни 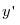 (x)=
(x)=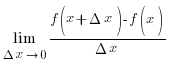
Мысал.
y=x2 функциясының x = 1 нүктедегі туындысын есептейік:
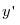 (x) =
(x) =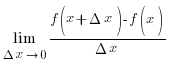
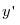 (x) =
(x) =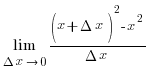
 (x) =
(x) =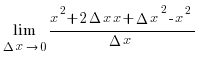
 (x) =
(x) =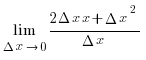
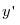 (x) =
(x) =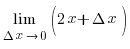
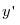 (x) = 2x
(x) = 2x
Сонымен ( x2 )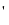 = 2x
= 2x
x=1, 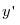 (1) = 2·1 = 2
(1) = 2·1 = 2