Лагранж және Коши теоремалары

Лагранж теоремасы

Егер y=f(x) функциясы:

1). [a; b] сегментінде аңықталған әрі үзіліссіз болса;

2). f ′ (x) туындысы осы сегментте шектелген болса;

Онда мына теңдікті қаңағаттандыратың (a; b) интервалына тиісті кем дегенде бір c нүктесі бар болады:

f(b) -f(a)=(b-a) ⋅ f ′ (c) c ∈ (a; b).

Коши теоремасы

Егер f(x) және g(x) функциялары:

1). [a; b] сегментінде аңықталған әрі үзіліссіз болса;

2). g′ (x),  f ′ (x) туындылары осы сегментте шектелген болса;

3). (g′ (x))²+ (f ′ (x))² ≠ 0, x∈ (a; b) үшін;

4). g(a) ≠ g(b);

Онда мына теңдікті қаңағаттандыратың (a; b) интервалына тиісті кем дегенде бір c нүктесі бар болады:

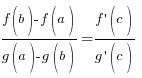, c ∈ (a; b).