Нақты санның дәрежесі. Санның 0 дәрежесі. Дәреже кестесі алгебра

Біз 5² = 5 ⋅ 5 = 25, 2³ = 2 ⋅ 2 ⋅ 2 = 8 екенің білеміз.

Дәл осылай a нақты санының n-ші ( n натурал сан ) дәрежесі деп мына aⁿ саның атаймыз:

aⁿ= a ⋅ a ⋅ a…⋅ a (n рет).

Мәселен

3⁴ = 3 ⋅ 3 ⋅ 3 ⋅ 3 ( 4 рет ) = 9 ⋅ 9 = 81,

2⁵ = 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ( 5 рет ) = 2 ⋅ 4 ⋅ 4 = 32

Санның 0 дәрежесі

Санның 0 дәрежесі үнемі 1 тең болады. Мысалы 5⁰ = 1 не 2⁰ = 1. Неге 1 тең? Мысалы 5⁰ дегенді математикада былай түсінеді:

5⁰ = 5^1-1 = 5¹/5¹ = 1

Санның 0 дәрежесі оны өзіне бөлу. Сондықтан 0 цифрда ондай дәреже, яғни 0⁰ дәрежесі болмайды. Өйткені 0 дегенді 0 бөлуге болмайды.

Дәреже кестесі алгебра

Мынандай дәреже кестесі алгебра сабақтарында келтіріледі:

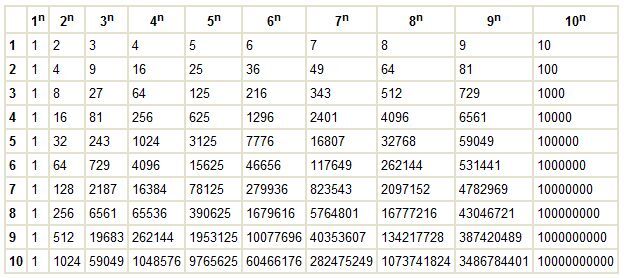
Оны пайдалану оңай. Мысалы 2 алтыншы дәрежесін табу керек болсын. Демек бізге керекті дәреже 2⁶. Ол үшін 2ⁿ бағанының (2ⁿ столбеці) және 6 қатарының (6 ряд) қиылысуы қараймыз:

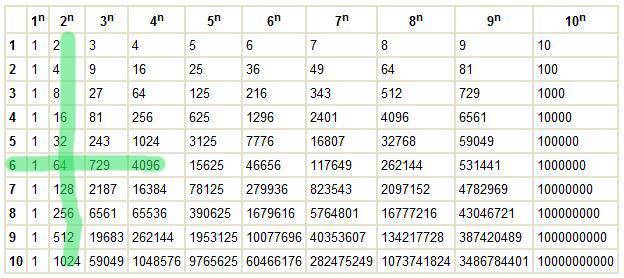
Осының қиылысында 64 тұр. Демек:

2⁶ = 64

Мына кесте көбейту кестесі сияқты. Қатар мен бағанның қиылысуында қажетті дәреженің мәні тұр.

Санның 1 дәрежесі

Кез келген санның 1 дәрежесі оның өзіне тең болады.

Дәреженің қасиеттері

Дәреженің анықтамасын пайдалана отырып мынандай ережелерді дәлелдеуге болады (бұл ережелер тек натурал санды дәрежелері үшін ғана емес сонымен қатар кез келген нақты санды дәрежелері үшін де орынды):

1) a^n+m = a ⁿ ⋅ a ^m

Мысалы 2²⁺³ = 2²*2³ = 4*8 = 32

2) (aⁿ)^m= a ^n⋅m

3) 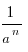 = a ^-n (a ≠ 0)

4) 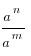 = a ^n-m (a ≠ 0)

5) a ⁰ = 1 (a ≠ 0)