Математикалық талдау
Математикалық талдау - үзіліссіздік, интеграл, туынды тәрізді ұғымдарды және олардың өзара байланыстарын зерттейтің ғылым. Бұл ғылым қазіргі математиканың ең ауқымды ғылыми бағыттардың бірі боп есептелінеді. Басқа атауы математикалық анализ ғылымы. Негізі екеуі қатар пайдаланып келеді.
Өйткені ғарышқа ұшырылған ракеталардың траекторияларың, атомдық реакторлардын реакцияларын, планеталар мен астероидтардың қозғалыстарын және көптеген басқа физикалық және химиялық процестерді зерттеуде математикалық талдаудың рөлі зор.
Математикалық талдаудың негізің қалаушылардың бірі көне грек оқымыстысы Архимед еді. Архимед математикалық анализдің идеяларын пайдалана отырып, адамзат тарихында тұнғыш рет пи саның математикалық жолмен есептеді. Бұл үшін Архимед шеңберге іштей және сырттай дұрыс n-бұрышты сызды:
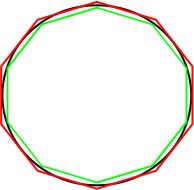
Ішкі n-бұрыштың периметрі шеңберден кіші ал сыртқы n-бұрыштың периметрі оның (шеңбердің) периметрінен үлкен болады деп есептеп, ол (Архимед) дұрыс 96-бұрышты салып, пи санының мынандай жуықтауын алды:
3+ 10/71 < pi < 3+ 1/7
Осы мысалда n саны артқан сайын аталған n-бұрыштардың периметрі шеңбердің периметріне жақындай береді деген ой қолданады. Бұндай жағдайда шеңбердің периметрі аталған дұрыс n-бұрыштардың n саны шексіздікке ұмтылғандағы шегі деп аталады.
Жаттығу. 1/k + 1 саны, k шексіздікке ұмтылғанда неге ұмтылады? Келесі сабақтарда шек, туынды, аңықталған интеграл, аңықталмаған интеграл тәрізді ұғымдары қарастырылады. Бұлардың бәрі шек ұғымына негізделеді.