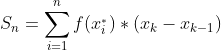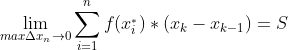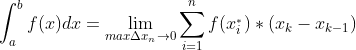Жоғарыдан y=f(x) функциясымен ал төменнен OX координат өсімен шектелген мына фигураның ауданың есептейік:
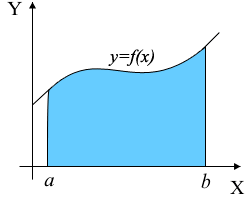
Бұл үшін [a; b] сегментің a=x0<x1<…xn-1<xn=b нүктелерімен [x0; x1], [x1; x2] ,…, [xn-1; xn] сегменттерге бөлейік те әрбір сегментте мынандай тіктөртбұрыштарды сызайық:
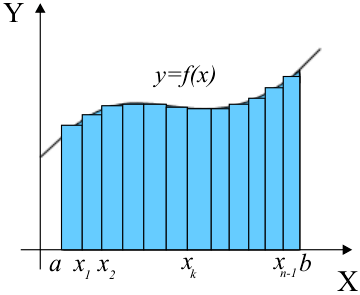
Бұл тікбұрыштардың жалпы ауданы аталған фигураның ауданына жуықтап алғанда тең болады.
Осы тікбұрыштардың жалпы ауданы Sn мынаған тең:
мұндағы xk* ∈ [xk-1; xk]
Тұжырым.
[x0; x1], [x1; x2] ,…, [xn-1; xn] сегменттерінің ең үлкенінің ұзындығы нөлге ұмтылғанда Sn саны аталған фигураның S ауданына ұмтылады, яғни мына шек орынды:
Анықтама
f(x) функциясының a және b аралығындағы анықталған интегралы деп мына шекті атаймыз:
Ньютон-Лейбниц формуласы
Егер f(x) функциясы [a; b] сегментінде үзіліссіз болса онда мына формула орынды:
мұндағы F′(x)=f(x)
Мысалы мына интегралды есептейік:
Қандай функцияның туындысы x тең?
F(x) = x2/2 + C
Себебі:
F'(x) = (x2/2 + C)’ = x
Жаттығулар
Ньютон-Лейбниц формуласын пайдалана отырып мына анықталған интегралдарды есептеңіз: