Функцияның шегі, үзіліссіз функция. Тамаша шек деген не?

x саны x₀ санына ұмтыла берсін, бірақ оған тең болмасын. Бұны x → x₀ деп белгілейміз.

Мысалы мына сандар тізбегінің n-ші мүшесі, n өскен сайын нөлге ұмтылады (бірақ нөлге тең болмайды):

,…

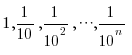Анықтама

A саны y=f(x) функциясының x→x₀ ұмтылғандағы шегі деп аталады, егер x₀ санына ұмтылған кез келген x₁, x₂, x₃,… сандар тізбегі үшін сәйкесінше f(x₁), f(x₂), f(x₃),… сандар тізбегі A санына ұмтылса.

Бұны 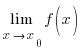= A деп белгілейді.

Мысалы

y = x² болса онда 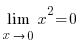. Өйткені нөлге ұмтылған кез келген x₁, x₂, x₃,… сандар тізбегі үшін x₁², x₂², x₃²,… сандар тізбегі де нөлге ұмтылады ғой.

Мына тамаша шектерді есте сақтау жөн:

1) 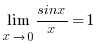 (бірінші тамаша шек).

2) 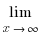(1+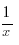) ^x = e, мұндағы e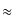2,718… (екінші тамаша шек).

Осы екі тамаша шекті жаттап алыңыз. Есеп шығарғанда жиі бұны пайдаланамыз. Тамаша шек формулалары бәлендей қиын емес. Тез жатталады.

Үзіліссіз функция

Анықтама

y=f(x) функциясы:

a) x₀ нүктенің белгілі бір маңайында анықталса.

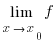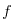b) (x)= (x₀)

Онда y=f(x) функциясы x₀ нүктеде үзіліссіз деп аталады.

Мысалы

y = x² функциясы x=0 нүктеде үзіліссіз, өйткені бұл функция біріншіден осы нүктенің аймағында анықталған, екіншіден 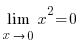, y(0) = 0, яғни 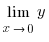(x) = y (0)

Анықтама

y = f(x) функциясы B сандар жиынының кез келген нүктесінде үзіліссіз болса, онда бұл y=f(x) функциясы B сандар жиынында үзіліссіз деп аталады.

Мысалы

y = x² функциясы нақты сандар жиынында үзіліссіз.

Жаттығу

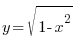функциясы [0; 1] сегментінде үзіліссіз бе?