Кейбір элементарлы функциялардың туындылар кестесі:
1. sin´x = cosx
2. cos´x = -sinx
3. tg ´x =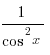 
4. ctg ´x =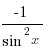 
5. (ax)´ =ln a · ax , мұндағы a>0, a = e болса онда (ex)´ = ex
6. (xn)´ = n · xn-1 , мұндағы n тұрақты сан
7. (lnx)´ =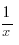 
8. (arcsinx)´ =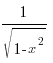 
8. (arccosx)´ =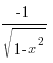 
9. (logax)´ =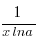 
10. (arctgx)´ =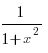 
11. (arcctgx)´ =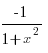 
Жаттығулар.
Туындылар кестесін және туындының қасиеттерің пайдалана отырып мына туындыларды есептеңіз:
a) y=x2+x+1, y′ -? b) y=x cosx, y′ -?
c) y=x sinx, y′ -? d) y=sin(2x), y′ -?
Енді бұл формулалардың біреуін дәлелдейік, мәселен бірінші туындыны дәлелдейік.
Дәлелдеуі:
1. sin´x = cosx
sin´x =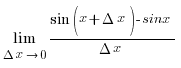 
мына формуланы пайдаланайық sin α – sin β = 2 sin(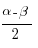
) cos(
):
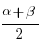sin (x+ Δ x) – sin x = 2 sin(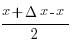
) cos(
)
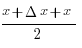sin (x+ Δ x) – sin x = 2 sin(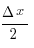
) cos(
)
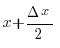Бұл өрнекті жоғарыдағы формулаға қоямыз:
sin´x =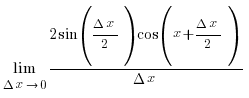 
sin´x =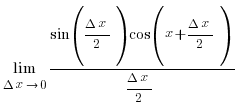 
бірінші тамаша шек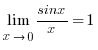 
бойынша
соңдықтан:
sin´x = cosx
Осы әдіспен cos´x = -sinx формуласын дәлелдеңіз
Жаттығу.
3 және 4 формулаларды (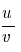
)´= 
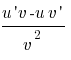ережесінің көмегімен дәлелдеңіз.
Есеп.
Екінші тамаша шектін көмегімен мына формуланы дәлелдеңіз (ex)´ = ex.
Туындылар кестесі туындыны есептеуде көп қолданылады соңдықтан бұл кестені есте сақтау жөн.