Туындыны алу ережелері

c-тұрақты сан u=u(x), v=v(x) болса онда мына формулалар орынды:

1). c´=0

2). (c · u(x))´=c · u´(x)

3). (u(x)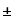 v(x))´=u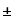´(x) v´(x)

4). (u(x)· v(x))´= u´(x)·v(x)+u(x)·v´(x)

5). ( u/v )´= ${u prime v-u v prime}/{v^2}$

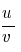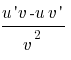
Дәлелдеуі:

1). c´=0

c´= 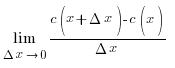lim{Delta x right 0}{{c(x+Delta x)-c(x)}/{Delta x}}

c´= lim{Delta x right 0}{{c-c}/{Delta x}}

c´= lim{Delta x right 0}{{0}/{Delta x}}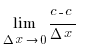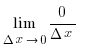

c´= 0

Жаттығу.

(c · u(x))´=c · u´(x) пен (u(x)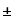 v(x))´=u´(x) 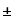v´(x) формулаларын дәлелдеңіз.

4). (u(x)· v(x))´= u´(x)·v(x)+u(x)·v´(x)

(u(x)· v(x))´= 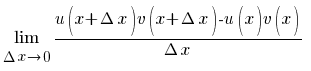lim{Delta x right 0}{{u(x+Delta x) v(x+Delta x)-u(x) v(x)}/{Delta x}}

(u(x)· v(x))´= lim{Delta x right 0}{{u(x+Delta x) v(x+Delta x)-u(x+Delta x) v(x)+u(x+ Delta x) v(x)-u(x) v(x)}/{Delta x}}

(u(x)· v(x))´= lim{Delta x right 0}{ } ( {{u(x+Delta x) v(x+Delta x)-u(x+Delta x) v(x)}/{Delta x}+{u(x+ Delta x) v(x)-u(x) v(x)}/{Delta x}} )

(u(x)· v(x))´= lim{Delta x right 0}{ } ( {u(x+Delta x) {v(x+Delta x)-v(x)}/{Delta x}+v(x) {u(x+ Delta x) -u(x)}/{Delta x}} )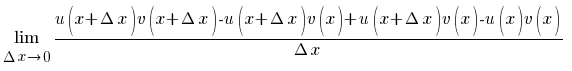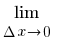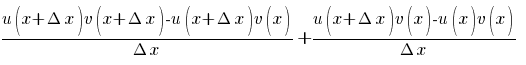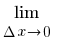

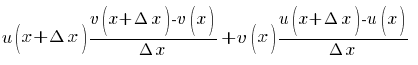(u(x)· v(x))´= u(x)·v´(x)+v(x)·u´(x)

(u(x)· v(x))´= u´(x)·v(x)+u(x)·v´(x)

Жаттығу

5-ші формуланы өз бетімен дәлелдеңіз.

Автор: Жандос Көксу