Арксинус
y=sinx функциясы x бұрышқа sinx санын сайкес қояды.
Мысалы x=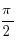
болса онда y=sin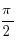=1.
Синус y=sinx функциясына кері функция арксинус деп аталады және x=arcsin y деп белгіленеді.
Мәселен sin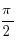=1 болғандықтан arcsin1= 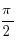болады.
Яғни арксинус дегеніміз бұрышты синустың мәнінен аңықтайтың функция.
Жаттығу.
arcsin0, arcsin(-1) -неге тең?
Тұжырым.
sinx=a теңдеуінің жалпы шешімі x=(-1)k arcsin a +2πk болады, k ∈ Z.
Мұндағы Z бүтін сандар жиыны, яғни k кез келген бүтін сан.
Мысалы.
sinx=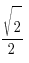
x=(-1)k arcsin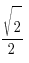 +2πk, k∈Z
arcsin=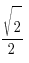
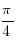
x=(-1)k 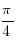+2πk, k∈Z
Жаттығу.
sinx=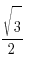
теңдеуінің жалпы шешімің аңықтаныз.
Арккосинус
y=cosx функциясы x бұрышқа cosx санын сайкес қояды.
Мысалы x=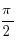 болса онда y=cos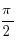=0.
Косинус y=cosx функциясына кері функция арккосинус деп аталады және x=arccos y деп белгіленеді.
Мәселен cos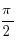=0 болғандықтан arccos 0 = 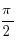болады.
Яғни арккосинус дегеніміз бұрышты косинустың мәнінен аңықтайтың функция.
Жаттығу.
arccos 1, arccos (-1) -неге тең?
Тұжырым.
cosx=a теңдеуінің жалпы шешімі x= ± arccos a +2πk болады, k ∈ Z.
Мысалы.
cosx=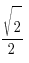
x= ± arccos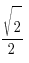 +2πk, k∈Z
arccos=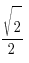
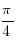
x= ± 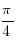+2πk, k∈Z
Жаттығу.
cosx=1/2 теңдеуінің жалпы шешімің аңықтаныз.