Егер шеңбер центрі координат остерінің қиылысуында жатса радиусы R тең шеңбер теңдеуі мынандай болады:
x2 + y2 = R2
Оның суреті мынандай болады:
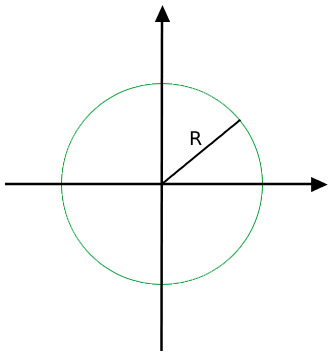
Мысалы шеңбер радиусы екі метрге тең болса оның теңдеуі мынандай болады: x2 + y2 = 4. Себебі екінің квадраты төртке тең. Осы шеңберді сызып көріңіз.
Центрі координат остерінің басында жатпаған жазықтықтағы шеңбер мына формуламен беріледі:
(x - x0)2 + (y - y0)2 = R2
Оның суреті мынандай:
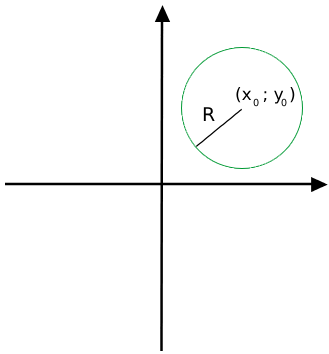
Демек соңғы формула центрі (x0; y0) нүктесінде жататын және радиусы R тең шеңбердің формуласы болып табылады.
Шеңберге есептер
x2 + 2x + y2 + 6y = 6 теңдеуі шеңберді сипаттайды ма?
x2 + 2x + y2 + 6y = 6
x2 + 2x + 1 + y2 + 6y + 9 = 6 + 1 + 9
x2 + 2*1*x + 12 + y2 + 2*3*y + 32 = 16
(x2 + 2*1*x + 12) + (y2 + 2*3*y + 32) = 42
(x + 1)2 + (y + 3)2 = 42
(x - (-1))2 + (y - (-3))2 = 42
Демек осы теңдеу центрі (-1; -3) нүктесінде жататын радиусы 4 тең шеңберді сипаттайды.
Жаттығу ретінде x2 - 4x + y2 - 2y = 4 теңдеуі шеңберге ие бола алатының тексеріндер. Оның центрі қандай? Ал радиусы ше?