Геометриялық прогрессия деген не? Геометриялық прогрессия формуласы

Геометриялық прогрессия деген не? Мысалы 2, 4, 8, 16 сандар тізбегі геометриялық прогрессия болады. Байқасаңыз 2 = 2*1, 4 = 2*2, 8 = 4*2, 16 = 8*2. Демек әрбір мүшесі 2 есейе береді. Тағы бір мысал 10, 100, 1000, 10000, 100000. Демек бірінші мүшесі 10, екіншісі 10*10 = 100 үшіншісі 100*10 = 1000. Осы жерде 10 көбейе береді.

Бірінші мүшесі b₁, екінші мүшесі b₂ = b₁ · q, үшінші мүшесі b₃ = b₂ · q ,…, n-ші мүшесі b_n=b_{n -1} · q болатын сандар тізбегі геометрикалық прогрессия деп аталады.

Мұндағы q -тұрақты сан.

Геометриялық прогрессияға мысалдар

a) 1, 2, 4,… сандар тізбегі геометрикалық прогрессияны құрайды.

Бұнда b₁=1, b₂=2, b₃=4, q=2. Шынымен де b₁=1, b₂=b₁·q=2 · 1=2, b₃=b₂·q =2 · 2=4.

Бұл прогрессияның жалпы заңдылығы b_n=b_n-1 · 2.

b) 3, 3/10, 3/100,… сандар тізбегі геометрикалық прогрессияны құрайды.

Бұнда b₁=3, b₂=3/10, b₃=3/100, q=1/10. Шынымен де b₁=3, b₂=b₁ ·q=3 · 1/10=3/10, b₃=b₂ ·q=3/10· 1/10=3/100.

Бұл прогрессияның жалпы заңдылығы b_n=b_n-1·1/10.

Геометрикалық прогрессия мүшелерінің қасиеттері

a) b_n²=b_n-1·b_n+1

b) b_n²=b_n-k·b_n+k , k ≤ n

S_n символымен геометрикалық прогрессияның алғашқы n мүшесінің қосындысын белгілейік.

Яғни S_n=b₁+b₂+…+b_n

Мысалы

Жоғарыдағы 1, 2, 4,… геометрикалық прогрессия үшін S₁=1, S₂=1+2=3, S₃=1+2+4=7.

Тұжырым

S_n=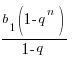

Егер |q|<1 болса онда S=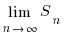=b₁+b₂+…+b_n+…+ шегі бар болады әрі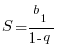

Геометриялық прогрессия формуласы осы. S_n табу үшін сонғы формуланы еске сақтап қойындар. Емтихан мен тесттілеуде ол жиір кездеседі.

Жаттығулар

a) 6, 12, 24,… прогрессиясының S₂, S₄ -ді есептеніз;

b) b₁=3, b₂=9, b₃=27 болса S₄ неге тең?