Логарифм деген не? Логарифм қасиеттері. Натурал логарифм және ондық логарифм

Мынандай теңдеу берілсін 2^x = 4. Осының шешімі қандай? x = 2 екені айдан анық. Бұл шешімді логарифм дейді. Және былай белгілейді:

log₂4 = 2

Логарифм анықтамасы

a^x =b теңдеуі берілсін, мұндағы a, b нақты сандар (a>0, b>0, a ≠ 1). b санының a негізі бойынша логарифмі деп x санын атаймыз және бұл санды log_a b деп белгілейміз:

a^x =b, x= log_a b

Логарифм мысалы

3^x =9

x= log₃9

Біз 3^x =9 теңдеуінің шешімі x=2 екенің білеміз ( 3² =9) соңдықтан log₃9=2.

Жаттығу

5³ =125 болса, log₅ 125 неге тең?

Логарифм қасиеттері

1) log_a (b ⋅ c)= log_a b+ log_a c

2) log_a ( 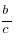)= log_a b- log_a c

3) log_a (bⁿ )= n⋅ log_a b (n- нақты сан )

4) log_a b= 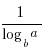(b≠ 1)

5) log_a b= 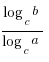(c≠ 1)

6) 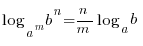(n, m- нақты сандар )

Ондық логарифм

Ондық логарифмнің негізі 10 саны болады. Яки 10^x = 1000 оны былай да x = log₁₀1000 және былай арнайы ол үшін етіп x = lg₁₀1000 былай да белгілейді. Бар айырмашылығы сол. Оған не үшін арнайы белгі жасап қойған? Себебі 10 дәрежелері физика, химия және басқа ғылымдарды жиі кездеседі. Қолданысы көп. Мысалы тоннаны килограмға аударғанда 10 дәрежелері қолданылады. Сондай есептерде 10 бар болған жерде ондық логарифм де бар болады.

Жаттығу ретінде lg₁₀100 саның табуды ұсынамыз. Прям прошу вас.

Натурал логарифм

Мынандай сан бар e = 2,7182... Ол π саны сияқты иррационал. Осы e саны негіз болатын логарифмді натурал деп атайды. Және ln деп белгілейді. Демек e^x = b болса x = lnb.