Мынау x2 - 2x + 1 = 0 квадраттық теңдеу боп табылады. Себебі белгісіз x шамасының квадраты тұр. Тағы бір мысал ол 3y2 - 4y + 1 = 0 теңдеуі. Мына жерде де белгісіз шаманың квадраты бар. Осы есепті шешу дегеніміз белгісіз айнымалыны табу.
ax2+bx+c=0 теңдеуі квадраттық теңдеу деп аталады, мұндағы a,b,c тұрақты сандар ал x белгісіз айнымалы.
Квадрат теңдеу формуласы жайлы теорема
ax2+bx+c=0 теңдеуінің D=b2-4ac дискриминанты оң болса ( D ≥ 0) онда осы теңдеудің екі x1 және x2 шешімі бар және олар мына формулалар арқылы аңықталады:
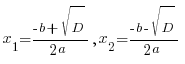
Демек квадрат теңдеу шешу үшін осы формуланы пайдалана аламыз. Енді бір мысал келтірейік. Сізге түсінікті болу үшін.
Мысалы
x2+4x-5=0
D=42 -4 ⋅ 1 ⋅ (-5)
D=16 +20
D=36 ≥ 0
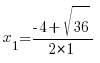
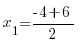
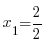
x1 = 1
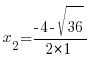
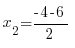
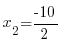
x2 = -5
Жауабы: x1 = 1, x2 = -5
Квадрат теңдеу есептері
Мына квадраттық теңдеулердің шешімдерін табындар (квадраттық теңдеулердің шешімдерін табатын формуланы пайдаланып):
a) x2+3x-4=0
b) x2-4x+4=0
c) y2+5y-6=0
d) x2-1=0
Квадраттық теңдеу дейді. Кейде квадрат теңдеу деп те атайды. Екі атау қатар жүріп тұр. Осы теңдеулер мектеп математикасында жиі кездеседі. Дискриминант теріс болса одан түбір ала алмаймыз. Демек ана формуланы пайдалануға болмайды. Нақты сандар өсінде.