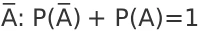Ақиқат оқиға мен мүмкін емес оқиға жайлы. Толық топ пен қарама-қарсы оқиға

Тәжірибе кезінде кейбір оқиғалар әрдайым пайда болады. Мысалы ойын сүйегін бір рет лақтырғанда 1, 2, 3, 4, 5 не 6 ұпай пайда болады. Бір оқиға құрастырайық. Мысалы A = "ойын сүйегін лақтырғанда 7 аз ұпай пайда болады" дегенді. Осы A оқиға әрқашан орындалып отырады.

Өйткені ойын сүйегін қанша лақтырмасақ та ұпай 7 аз болады. Ол 20 не 100 бола қалмайды. Осыны ақиқат оқиға деп атайды. Ол тәжірибе кезінде әрқашан пайда болатын оқиға. Ойын сүйегін сан мәрте рет лақтырсақ та ол 7 аз болады.

Мүмкін емес оқиға

Тәжірибе кезінде ешқашан пайда бола алмайтын оқиғалар да бар. Мысалы B = "ойын сүйегінің ұпайы 30" дегені. Осыны мүмкін емес оқиға деп атайды. Ол ешқашан пайда болмайды. Өмірде ондай оқиғалар көп. Мысалы жер бетінде температураның -150 градус болуы.

Немесе адамның 200 жасқа толуы. Рас ондай жайттар көне жыр мен ертегілерде бар. Бірақ қазіргі заманда ондай адамдар жоқ. Математикалық модель құрғанда адам жасы әдетте 1-150 жыл арасында алынады.

Толық топ

Ойын сүйегін лақтырғанда 1, 2, 3, 4, 5, 6 ұпайлардың біреу пайда болады. Былай белгілейік. B₁ = { 1 }, B₂ = { 2 }, B₃ = { 3 }, B₄ = { 4 }, B₅ = { 5 }, B₆ = { 6 }. Демек әрбір B оқиға ол ойын сүйегінің түсуі. Ойын сүйегін бір мәрте рет лақтырғанда ең болмаған бір "B" оқиғасы пайда болады. Ол B₁ не B₃ не басқа біреуі болуы мүмкін. Қайсы екені белгісіз әйтеуір біреуі пайда болады.

Тәжірибе кезінде A₁, A₂, ..., A_n ең болғанда біреуі пайда бола алатындай болса осы оқиғалар тізімі толық топ деп аталады.

Толық топ құрайтын оқиғалар үшін мынандай формула орынды:

P(A₁) + P(A₂) + ... + P(A_n) = 1

Яғни олардың ықтималдықтарының қосындысы бірге тең. Осыны B₁-B₆ оқиғалар тобы үшін тексеріңіз.

Қарама қарсы-оқиға

Жүз теңгелікті бір рет лақтырсақ не "100 теңге" не "елтаңба" жағы пайда болады:

Осы екі оқиғаның біреуі ғана пайда болады. Екеуі емес. Екі оқиға бірікпейді. Екеуі әрқилы.

Тағы бір мысалы Манчестер мен Ливерпуль командалары ойнап біреуі жеңіске жетсін. Ол не Манчестер не Ливерпуль. Екеуінің бірі.

Осындай оқиғаларды қарама қарсы деп атайды. Екі бірікпейтін және толық топ құратын оқиғалар біріне бірі қарама қарсы деп аталады. Мысалы A = "100 теңге" ал B = "елтаңба" деп белгілесек осы екі A және B оқиғаларының біреуі ғана пайда болады. Демек олардың қорытқы ықтималдығы бірге тең:

P(A) + P(B) = 1

Ғылыми ортада қарама қарсы оқиғаларды бір әріппен белгілеуге дағдыланған. A оқиғасына қарама қарсы оқиғаны дәле осы әріппен белгілейді тек оның үстіне сызық қоя салады: