a және b векторларының:
1). a+b қосындысы деп координаттары {ax+bx ; ay+by} болатын c векторын атаймыз.
2). a – b айырымы деп координаттары {ax – bx ; ay– by} болатын d векторын атаймыз.
3). a векторының k санға көбейтіндісі деп {k · ax ; k · ay} векторын атаймыз және k · a деп белгілейміз.
Векторларды қосу
a және b векторларының a+b қосындысын параллелограмм ережесі бойынша есептеуге болады.
Бұл үшін бұл векторларды сызайық:
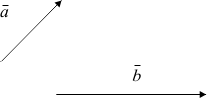
a+b қосындысын есептеу табу үшін a -нің ұшына b -нің басын орналастырамыз:
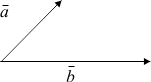
Бұл схеманы параллелограммға дейін толықтырамыз:
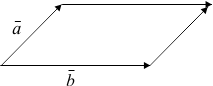
a+b қосындысы, басы a-нің басымен ал ұшы b-нің ұшымен сәйкес келетің вектор болады:
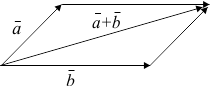
Соңғы схема бойынша a+b қосындысы сызылған параллелограммның диагоналіне тең болады, соңдықтан бұл әдісті параллелограмм ережесі деп атайды.
Векторларды алу
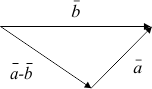
a және b векторларының a – b айырымын есептеу үшін үшбұрыштар ережесі пайдалынады:
Бұл үшін бұл векторларды сызайық:

a -нің және b -нің ұштарын біріктірейік:
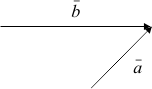
a– b айырымы, басы a-нің басымен ал ұшы b-нің басымен сәйкес келетің вектор болады: