B1, B2,..., Bn оқиғалары толық топ құрсын. Олардың арқасында пайда болуы мүмкін A оқиғасы бар болсын. Осы шарттар орындалса мына Байес формуласы орынды болады:
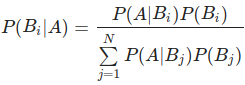
Байес теоремасына есептер
Осы формуланы Байес теоремасы деп те атап жатыр. Екеуі қатар айтылады. Осыған арнап бірнеше есепті шығарып көрейік.
Екі адам жамбы атудан сайысып жатыр. Қабанбай батыр мен Қасым-Жомарт деген шал. Біріншісінің садағының оғының жамбыға тию ықтималдығы 95 пайыз (0,95). Екіншісі көзі жөнді көрмейтін әрі қолында қуаты жоқ шал оның нысанаға тию ықтималдығы бар жоғы 1 пайыз (0,01).
Екі садақшы бір рет атты. Бір оқ нысанаға тиді ал екіншісі айдалаға кетті (байқамай, жақын жерде жүрген Нұрсұлтанға тиді). Қабанбай батыр оғының нысанаға тигенінің ықтималдығы қандай?
B1 деп Қабанбай батыр тиді ал B2 деп шал тиді деп белгілейік. Есептің шарты бойынша осы екі оқиға толық топ құрады және олардың пайда болу ықтималдығы бірдей:
P(B1) + P(B2) = 1
P(B1) = P(B2)
P(B1) + P(B2) = 2P(B1) = 1
P(B1) = 1/2 = 0,5
Қабанбай батырдың нысанаға тию ықтималдығы 90 пайыз ал шалдың бар жоғы 1%. Демек мыналар орынды:
P(A | B1) = 0,95
P(A | B2) = 0,01
Енді құрметті, барша жырларда жырланатын, ел қорғаны, ел мақтанышы бола алған, атағы зор батырымыздың нысанаға тию ықтималдығын Байес формуласына салып оңай таба аламыз:
P(B1 | A) = 0,95*0,5/(0,95*0,5 + 0,01*0,5) = 0,99
Демек 99 пайыз! Бұған ұқсамайтын басқа нәтиже кім күтті? Шалдың ықтималдығын да есептеп қою керек. Әйтпесе біреу мені қорладын деп реңжіп қалады!
P(B2 | A) = 0,01*0,5/(0,95*0,5 + 0,01*0,5) = 0,01
Какой пазор!