Векторлардың скаляр көбейтіндісіне мысалдар мен есептер

Жазықтықтағы векторлар екі санмен сипатталады. Мысалы былай a = {2, 1} не былай b = {4, 2}. Әрбір вектор екі санмен сипатталады. Сондықтан екі векторды көбейте аламыз, былай 2*4 + 1*2 = 8 + 2 = 10.

Анықтама

a = (a_x, a_y) және b = (b_x, b_y) векторларының (a, b) скаляр көбейтіндісі деп a_x· b_x + a_y· b_y саның атаймыз:

(a, b) = a_x · b_x + a_y · b_y

Мысалы a = {1, 3}, b = {4, 2} болса, онда (a, b) = 1·4 + 3·2 = 4 + 6 = 10.

Кейде скаляр көбейтінді деп те аталады. Мағынасы бір. Скаляр көбейтінді формуласын жаттап алындар не жазып алындар. Осы формуламен көп есеп шығарылады.

Скаляр көбейтіндінің қасиеттері

Векторлардың қасиеттерін және скаляр көбейтіндінің анықтамасын пайдаланып мынандай формулаларды қорыта аламыз:

1). (a, b) = (b, a)

2). (a, a) = |a|²

3). (a+b, c) = (a, c) + (b, c)

4). (a –b, c) = (a, c) -(b, c)

5). (k ·a, b) = (a, k ·b)=k ·(a, b)

Скаляр көбейтіндісінің геометрикалық интерпретациясы.

a және b векторларының (a, b) скаляр көбейтіндісі бұл векторлардың модульдерінің осы векторлардың арасындағы бұрыштың косинусының көбейтіндісіне тең.

Яғни (a, b) =|a| · |b| cos∠(a, b),

мұндағы ∠(a, b) дегеніміз a және b векторларының арасындағы бұрыш:

 

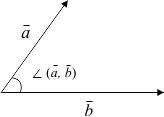
Векторлардың скаляр көбейтіндісіне есептер

Мына есептер векторлардың скаляр көбейтіндісі сабағына арналған. Осыларды шығарып көріңдер. Жоғарыдағы формуланы пайдаланып.

1) a = {10, 3}, b = {2, 2}, (a, b) – ?

2) a = {2, 7}, b = {5, 2}, (a, b) – ?

3) a = {150, 30}, b = {250, 240}, (a, b) – ?

Кеңістіктегі векторлардың скаляр көбейтіндісі

Кеңістікте векторда үш координат бар болады соларға қатысты скаляр көбейтінді де анықталады. a = (a_x, a_y, a_z) және b = (b_x, b_y, b_z) векторларының (a, b) скаляр көбейтіндісі былай анықталады:

(a, b) = a_x · b_x + a_y · b_y + a_z*b_z

Кеңістіктегі векторлардың көбейтіндісі жазықтықтағыдай қасиеттерге ие.