Виет теоремасы және квадраттық теңдеулер

ax²+bx+c=0 (a≠0) квадраттық теңдеуінің D=b²-4ac дискриминанты оң болғанда бұл теңдеудің екі 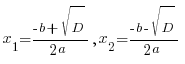шешімі бар болатының квадраттық теңдеу сабағында айтылған.

Бұл формулалар теңдеудің шешімдерін теңдеудің коэфициенттері арқылы табуға мүмкіндік береді.

Кері жағдайда, яғни x₁ пен x₂ белгілі ал a,b,c белгісіз болғанда Виет теоремасын қолдана аламыз:

Виет теоремасы

ax²+bx+c=0 теңдеуінің шешімдері x₁ пен x₂ болса онда мына формулалар орынды:

x₁·x₂=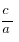

x₁+x₂=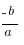

Мысалы x₁=1, x₁=3 ал теңдеуіміз белгісіз болсын, Виет теоремасы бойынша:

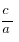=x₁·x₂=1·3=3

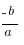=x₁+x₂=1+3=4

ax²+bx+c=0 теңдеуінің x²+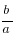x+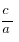=0 теңдеуіне эквиваленттігін пайдалансақ онда біздің теңдеуіміз мына түрге келеді:

x²+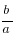x+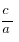=x²-4x+3

Яғни x²-4x+3=0.

Ескерту.

a=1 десек онда ax²+bx+c=0 теңдеуі x²+bx+c=0 теңдеуіне айналады және Виет теоремасы мынандай болады:

x₁·x₂=c

x₁+x₂=-b.

Жаттығулар.

a). x₁=3, x₂=4, a=2. ax²+bx+c=0-? b). x₁=2, x₂=5. x²+ax+b=0-?