Ойын сүйегін көп рет лақтырсақ не болады? Бір рет лақтырғанда 1 ден 6 дейін ұпай пайда болады. Мысалы бір рет лақтырғанда 2 ал екінші рет 4 болса олардың орташа мәні (2 + 4)/2 = 3.
Ал он не мың рет лақтырғанда орташа ұпай қандай болады? Ойын сүйегінің үлестірім кестесі мынандай (X кездейсоқ шаманың мәні ал p оның ықтималдығы):
| X | 1 | 2 | 3 | 4 | 5 | 6 |
| p | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
Оның математикалық үмітін есептеп көрейік. Ол үшін M(X) = x1*p1 + x2*p2 +...+ xn*pn формуласын пайдаланамыз:
M(X) = 1*1/6 + 2*1/6 + 3*1/3 + 4*1/6 + 5*1/6 + 6*1/6
M(X) = 7/2 = 3,5
Осы ойын сүйегін мың рет лақтырсақ оның орташа ұпайы (барша түскен ұпайларды қосындысының лақтыру санына бөліндісі) осы математикалық үмітке, демек 3,5 санына жақындайды екен. Ұмтылады-мыс:
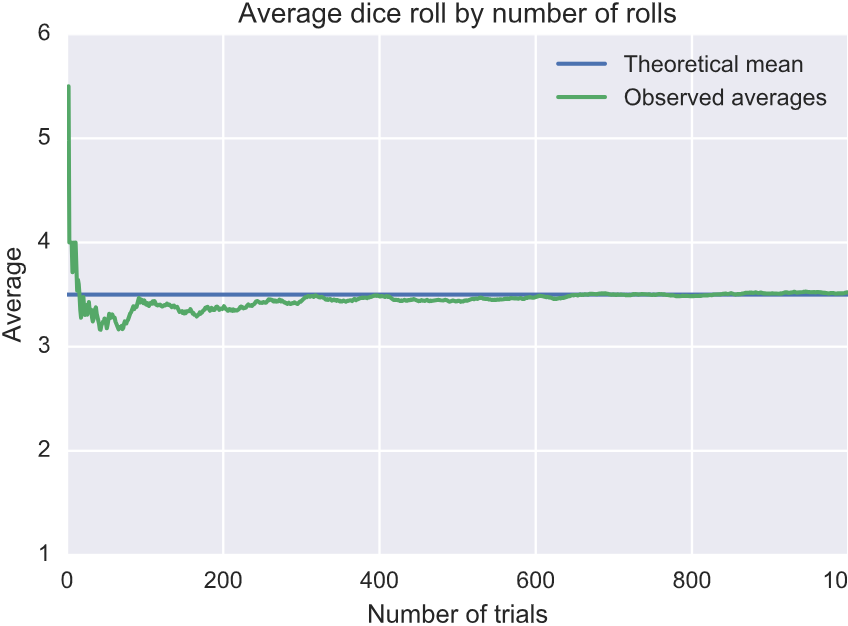
Үлкен сандар заңы
Ықтималдықтар теориясында "үлкен сандар заңы" дегені бар. Ол тәжірибе саны тым көп болғанда кездейсоқ шаманың қандай мәнге жақындайтының анықтайтын теоремалардың жиынтығы.
Марков теңсіздігі
Егер X кездейсоқ шамасы оң мән қабылдаса және оның M(X) математикалық үміті бар болсын. Кез келген a > 0 саны үшін мына теңсіздік орынды:
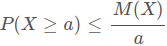
Осыны Марков теңсіздігі деп атайды. Кездейсоқ шаманың математикалық үміті белгісіз болғанда осы теңсіздіктің көмегімен кейбір есептерді шығара аламыз.
Мысалы Алматы қаласы күн сайын 700 000 текше метр су тұтынып жатыр (2022 жылы). Осы жұрттың 1 000 000 текше метр су тұтына қалуының ықтималдығы қандай?
Осы жерде M(X) = 700 000. a = 1 000 000. Демек мынандай теңсіздік орынды:
P(X ≥ 1 000 000) ≤ 7 00 000/1 000 000
P(X ≥ 1 000 000 ) ≤ 0,7
Яғни Алматы қаласы бір миллион текше метр су тұтына қалатының ықтималдығы 0,7 аз.
Жаттығу ретінде Астана қаласындағы су тұтыну көлемі 500 000 текше метр шамасына жету ықтималдығын табындар. Қазір Астана қаласында күн сайын 300 000 текше метр су тұтынылады (2023 жылы).
Чебышев теңсіздігі
X кездейсоқ шамасының математикалық үміті M(X) пен D(X) дисперсиясы бар болсын әрі шектеулі болсын. Осы шарттар орындалса кез келген a > 0 үшін мынандай теңсіздік орынды:
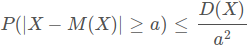
Осыны Чебышев теңсіздігі деп атайды.
Чебышев теоремасы
Егер X1, X2, ..., Xn кездейсоқ шамалардың дисперсиясы бір санмен шектелген болсын. Егер n шексіздікке ұмтылса кез келген e > 0 саны үшін мынандай теңдік орынды:
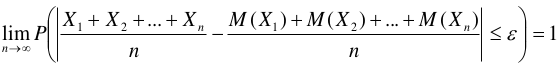
Яғни кездейсоқ шамалардың орташа мәні олардың математикалық күтімнің орташа мәніне жақындай береді.
Салдары
Егер X1, X2, ..., Xn шамаларының математикалық үміті бірдей. a тең болса (M(X1) = M(X2) = ... = M(Xn) = a) ал дисперсиялары бір C сандан аз болса мынандай теңсіздік орынды:
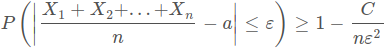
Ойын сүйегін бір рет лақтырғанда түсетін ұпай өзі кездейсоқ шама. Оны X1 деп белгілеуге болады. X2 екінші рет. X3 үшінші рет және Xn ойын сүйегін n рет лақтырғандағы пайда болатын ұпай саны деп белгілеуге болады.
Демек ойын сүйегін көп рет лақтырғанда оның орташа мәні математикалық күтімге жақындай береді.