Тригонометриялық теңдеулер

Ізделінетің белгісізі тригонометрикалық функцияның аргументіне еңетің теңдеулерді тригонометриялық теңдеулер деп атайды.

Мысалы cos²x+cosx-2=0 теңдеуі тригонометрикалық теңдеуі болады.

Бұл теңдеуді шешу үшін cosx=t алмастыруын еңгіземіз:

cos²x+cosx-2=0

cosx=t

t²+t-2=0 (квадраттық теңдеу)

t₁=-1

t₂=-2

cosx=-1

x=±arccos(-1)+2πk, k∈Z (Z-бүтін сандар жиыны) (арксинус пен арккосинус)

x=±π+2πk, k∈Z

cosx ≠ -2

Сонымен cos²x+cosx-2=0 теңдеуінің шешімдері x=±π+2πk, k∈Z болады.

Кейбір тригонометриялық теңдеуді шешу үшін қосымша түрленулерді жасау қажет болады.

Мысалы sin²x+4cosx-1=0 теңдеуін шешу үшін sin²x=1- cos²x формуласын пайдалану қажет:

sin²x+4cosx-1=0

sin²x=1- cos²x

1- cos²x+4cosx-1=0

– cos²x+4cosx=0

cosx (4-cosx)=0

x=±arccos0+2πk, k∈Z (Z-бүтін сандар жиыны)

x=±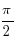+2πk, k∈Z

4-cosx=0

cosx ≠ 4

Жауабы: x=±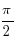+2πk, k∈Z

Ал кейбір есептерде жаңа айнымалыны да қосымша түрленулерді де еңгізу қажет болады.