Теңдеу деген не? Мысалы x + 1 = 2 теңдеу болып табылады. Теңдеу дегеніміз ол белгісіз айнымалысы бар теңдік. Осының шешімін табайық (сайтта квадраттық, тригонометриялық, биквадрат, көрсеткіштік сияқты теңдеулерді шешу жолдары көрсетілген сабақтар бар):
x + 1 = 2
x = 2 - 1 (1 теңдіктін сол жағынан оң жағына ауыстырамыз, сонда оның таңбасы минуске ауысады)
x = 1
Тағы бір теңдеуді келтірейік. Ол мынандай шағын теңдеу 2x + 2 = 6. Оның шешімін қалай табамыз? Оны былай есептеп шығарамыз:
2x + 2 = 6
2x = 6 - 2 (2 сол жақтан оң жаққа -2 боп ауысты)
2x = 4
2x/2 = 4/2 (теңдеудің екі жағын 2 бөлеміз)
x = 4/2 = 2
Жаттығу ретінде мына 3x + 2 = 8 теңдеудің шешімін табуды сізге тапсырамыз.
Теңдеуді шешу
Теңдеуді шешу үшін неше түрлі әдістер пайдалану керек. Мысалы теңдіктін екінші жағына сандарды ауыстыру. Теңдеудің екі жағын бір санға бөлу. Квадратқа алу не түбір алу және тағы сол сияқты амалдарды қолдану.
Сызықтық теңдеу
Сызықтық теңдеу деп a·x+b=c типті теңдеуді атайды, мұндағы a,b,c тұрақты сандар ал x ізделінетің белгісіз.
Мысалы 2x + 1 = 7 теңдеуі.
Бұндай теңдеуді былай шешеді:
2x + 1 = 7
2x = 7-1
2x = 6
x = 6/2
x = 3
Жаттығулар.
Мына сызықтық теңдеулерді өз бетімен шешіңіз:
a) x + 1 = 4
b) 2y -3 = 1
c) -z + 3 = 4
d) 5x -5=20
ax+b=c типті теңдеудің жалпы шешімі:
ax+b=c
ax=c-b
x=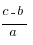
Тарихи мағлұмат
Осыған ұқсас сызықтық теңдеулерді шешудің жалпы жолдарын, адамзат тарихында тұнғыш рет, шыққан тегі Орта Азиялық Әл-Хорезми ашқан. Әл-Хорезмидің еңбектері математиканың дамуына зор серпіліс, үдеу берген, бұны жоғары бағалаған кейінгі математиктер, оның ( Әл-Хорезмидің ) құрметіне математиканың бір саласын «Алгебра» деп атай бастаған.
Теңдеулер неше алуан болады. Квадраттық, кубтық, тригонометриялық және тағы басқалары. Мектептегі математика бағдарламасының басым бөлігі теңдеулермен байланысты. Физика мен химия пәндерінде де олар бар.