Дискретті кездейсоқ шамалар кесте арқылы беріле алады. Мысалы ойын сүйегінің ұпайлары 1 ден 6 дейін ғана өзгере алады. Солардың математикалық үмітін есептегенде кездейсоқ шаманы оның ықтималдығына көбейтіп қоса салдық.
Ал үзіліссіз кездейсоқ шамалардың математикалық үміті мен дисперсиясын олай есептей алмаймыз. Себебі саны шексіз. Оны үлестірім тығыздығының интегралдары арқылы есептейміз.
Үзіліссіз кездейсоқ шаманың математикалық үміті
Үзіліссіз кездейсоқ шаманың үлестірім тығыздығы f(x) болсын. Осының математикалық үміті деп мына интегралды атаймыз:
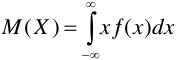
Мысалы мынандай үлестірім тығыздығы бар кездейсоқ шаманың математикалық үмітін есептеп көрейік:
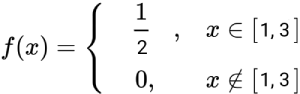
Ең алдымен математикалық үміттін анықтамасын пайдаланып мынандай интегралды есептейік:
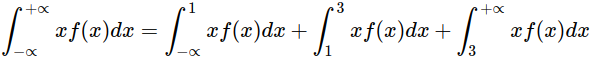
Осы интеграл математикалық үмітке тең. Оның сол жағындағы екі интеграл 0 тең. -∞ тен 0 дейін және 3 тан +∞ дейінгілері:
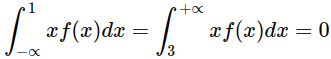
Себебі осы аралықтарда f(x) = 0. Демек математикалық үміт былай табылады:
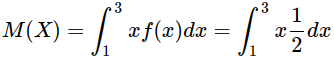
Соңғы интегралдың алғашқы бейнесі x2/4 функциясы болады. Интегралдар кестесін пайдаланып соған көз жеткізе аласыз. Алғашқы бейнесі табылғаннан кейін Ньютон-Лейбниц формуласы бойынша математикалық үмітті таба аламыз:
M(X) = 32/4 - 12/4 = 2
Дискретті математикалық үміт сабағында айтылған барша қасиеттер үзіліссіз кездейсоқ шама үшін де орынды.
Үзіліссіз кездейсоқ шаманың дисперсиясы
Кездейсоқ шаманың үлестірім тығыздығы бар болса математикалық үмітпен қатар дисперсияны да таба аламыз. Осы дисперсия мына формула арқылы табылады:
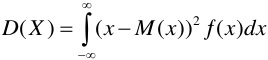
Бұдан басқа формула да орынды:
D(X) = M(X2) - M2(X)
Дискретті кездейсоқ шаманың дисперсиясы деген сабақтағы оның қасиеттері үзіліссіз кездейсоқ шама үшін де орынды. Жаттыығу ретінде жоғарыдағы үлестірім тығыздығының дисперсиясын тауып көріндер.
Орташа квадраттық ауытқу
Дисперсиядан квадраттық түбір алсақ бір сан пайда болады. Оны орташа квадраттық ауытқу деп атайды және σ әрпімен белгілейді:
D(X) = σ2